Ordered Prediction Markets
Say you want to know how many Tesla cars will be sold next year.
You can make a prediction market on this question and let people trade based on the outcome. One way is to pick a likely value (say 400 thousand) and ask for the probability the outcome will be higher than this, creating a "boolean" prediction market. Another way is to simply ask for the expected value, creating an "index" prediction market. I propose a third approach which asks for the full cdf of outcomes.
Boolean markets:
To make the answer robust to tricks, all three approaches put money on the line. In the first approach we want users to say a probability between 0 and 1.
If Alice thinks the probability that Tesla makes fewer than 400K cars (YES) is 70% and Bob thinks it's 80% then we want to help them make a deal that they both expect to profit from. If Bob promises to pay $1 in the event of NO then Alice is willing to pay $0.30 (or less) for this. Similarly, Bob will pay $0.80 (or less) for a contract paying $1 in the event of YES.
Alice and Bob might not trust each other, so instead of Alice paying Bob and worrying that Bob might run away (or run out of money), they both give the money to us (the prediction market) and we give it to the winner when we learn the outcome. Only one of YES and NO can happen and we only need to pay out $1, so instead of charging them $0.30 and $0.80 we charge some smaller values that add to $1. For example, $0.25 and $0.75.
One important point here is that people don't input bets at specific probabilities, but on ranges like "> 70%" or "< 80%". If you think the probability is more than 70% you make different deals than if you think it's less than 70%.
Index markets:
It often happens that the outcome becomes very certain in a boolean market but we want more information. Tesla may produce 400K cars after half the year, making the probability go to 100%, but we still want to know how many cars they will produce. To handle this we can introduce an "index" market. Now Alice and Bob say the outcome they expect (as in their expected value). Just like before, when their numbers differ there is a deal to be made.
The only wrinkle is that we can't just give the "winner" $1 because that would be a boolean market like before. Instead we give someone money proportional to the outcome. For example, we could give Alice $1 for every car Tesla makes, but in the real world we would scale this down to something reasonable like $1 for every million cars (rounded to the nearest $0.01). If Alice thinks the expected value is 500K and Bob thinks it's 400K then Alice can pay $0.45 to Bob and Bob will pay Alice $1 for every million cars.
Again, we don't want Bob to run away without paying so we hold the money for Alice. But what if Tesla produces a billion cars and we didn't charge enough for this outcome? To prevent this sort of thing we put an upper bound M on the payout and only take M (minus $0.45) from Bob.
Ordered markets:
In the real world index markets are often implemented as a collection of boolean markets at different outcomes. For example, a boolean market for "Will Tesla produce more than X*100K cars" for each X in 1 to 10. This can be nice because we see the whole distribution function of outcomes. Here's another approach:
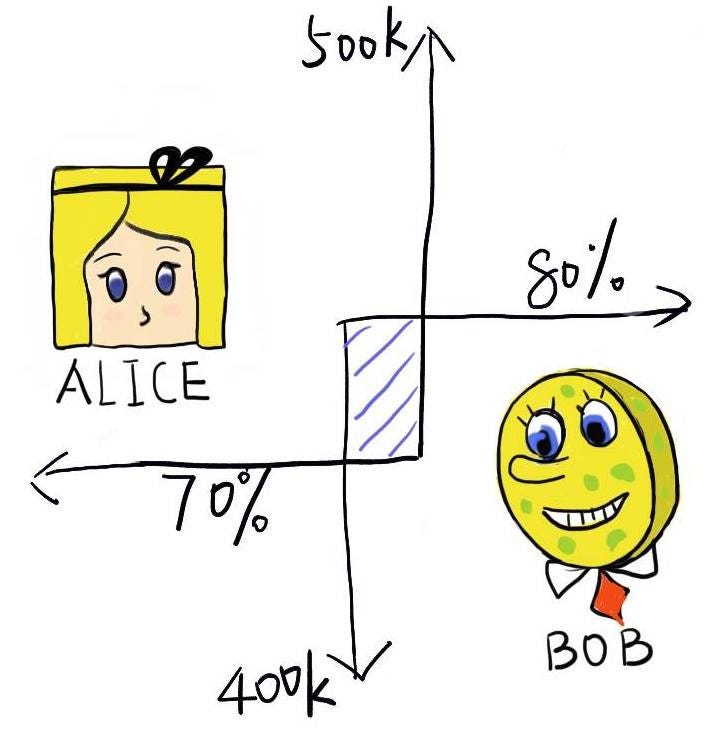
Say Alice thinks that Tesla has a 70% chance of making fewer than 500K cars. Bob, on the other hand, thinks there's a 80% chance of making fewer than 400K cars. These beliefs are incompatible so they'd be willing to make a deal at, say, a 75% chance of fewer than 450K cars. Then we can generate a boolean contract for them with these two parameters.
This provides several advantages. First, it elicits more information than the index market while simplifying the process of market creation that might happen with several related boolean markets. It yields potentially beautiful and easily readable graphs showing the cdf of the outcome. In a boolean or index market there are usually many offers at different prices. When we draw a curve of how many offers there are at each price (the density) we see how robust the current price is.
We can draw something similar for ordered markets, visualizing the offer density as a heatmap instead of a curve.
Ordered markets also guarantee consistency between related boolean markets. In the real world sites like PredictIt quite often have markets with inconsistent values on a single question. It allows thinking of the value as log-distributed without changing the underlying mechanism at all. Lastly, I claim it "thickens" order books by allowing a user to participate in several markets at once. I'll expand on this below.
Order matching:
To implement boolean and index markets, one user, say Alice, comes along first and says "more than 30%", then Bob comes along later and takes the deal. Let's call Alice's action a "limit order". An interface for this market might allow Bob to enter "less than 20%", instantly match Bob with Alice at Alice's price, and create a limit order only if no user can immediately make a deal with Bob.
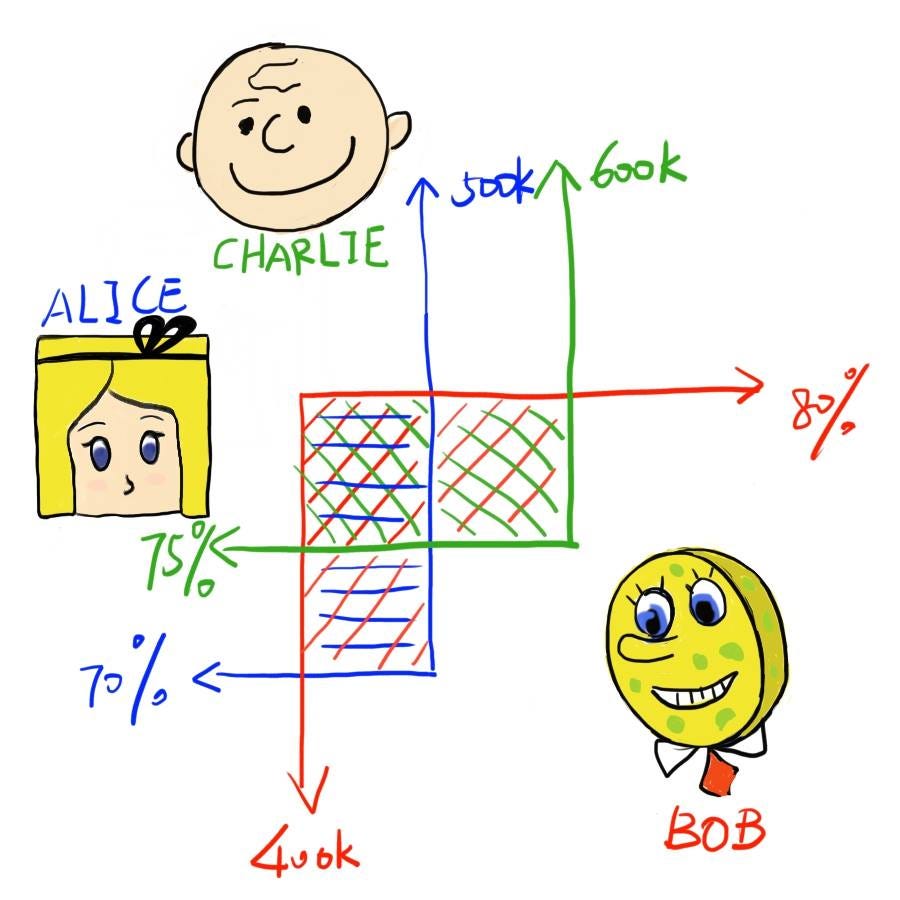
The process of checking who Bob would make a deal with is very easy for boolean and index markets. If Bob has a "less than" claim (a sell order) then he always wants to make a deal with the "more than" claim (the buy order) with the highest value. That is, he always wants to sell for the highest price. But when Bob makes a claim like (>80%, <400K) he can be matched with either Alice at (<70%, <500K) or some other user Charlie at (<75%, <600K). It isn't clear which of these Bob prefers without asking Bob for more information about his curve. I would prefer to implement this by treating the probability as the price and always taking the best probability (in this case Alice), but the choice is a little arbitrary.
Generally markets form the contract at Alice's price (the limit order price) because a rational user could simply look at the list of open orders and bid this price. For ordered markets this principle says that the deal should be both at the limit order price (70%) and at the limit order value (500K).
Another interesting feature of order matching is that because it's so simple in the 1-dimensional case it can be done in constant amortized time. With ordered pairs as I've described it can be done in O(log(n)) time, but in practice this is probably overkill.
Reselling contracts:
One major advantage of boolean and index markets is that contracts can be resold when more information becomes available. Once Alice and Bob form a contract, giving a YES share to Alice and a NO share to Bob, Alice can then resell her YES share to Charlie and stop waiting for the outcome. In practice this means that users can exchange millions of dollars predicting the number of cars Tesla will produce while we, the market maker, hold on to only tens of thousands. Similarly, an index market produces normal shares (where the holders gets paid the number of cars) and "negative" shares (where the holder gets paid (M - the number of cars)).
As soon as Alice owns both a YES and NO share a website will pair them up, give Alice $1, and remove both shares. By contrast, an ordered market generates shares for many different boolean questions and it isn't immediately clear how these would be paired. In fact if Alice has shares for (> 500K) and (<= 400K) these cannot cancel (the value could resolve as 450K). But if she has (> 400K) and (<= 500K) then she is guaranteed $1. The site can immediately pay this and leave Alice with a promise of $1 in the range (400K, 500K]. It’s not quite as clean but still allows some multiplier of trading volume over reserved cash.
Betting a curve:
Finally, we can imagine many variations on this scheme. We have implicitly treated a bet like (<70%, 500K) as a step function upper bounding the cdf of the outcome. We can allow arbitrary functions as lower or upper bounds and create a deal whenever a lower bound crosses an upper bound. This isn't just pointless generalization. I believe the key advantage of an ordered market is in "thickening" the order book by making a limit order apply to multiple values. If Alice bets on a whole curve f(x) for the lower bound then Bob can take the deal at f(400K) or f(500K). This allows Alice to pay once and have two orders open at the same time.
Now, I wouldn't recommend anything too fancy for arbitrary curves in practice. For one thing, they increase the complexity of order matching and make the user interface more complicated. They also run the risk of floating point errors that could be devastating if real money is on the line. I believe step functions would be practical and useful though. Say Alice bets on A at (<70%, 500K) and a smaller amount B at (<80%, 600K). We write the step function for these two points and create a limit order for this curve with value A, then add a second limit order for A-B with just the point (<70%, 500K).
Thank you for coming to my TED talk.